Երկրաչափություն

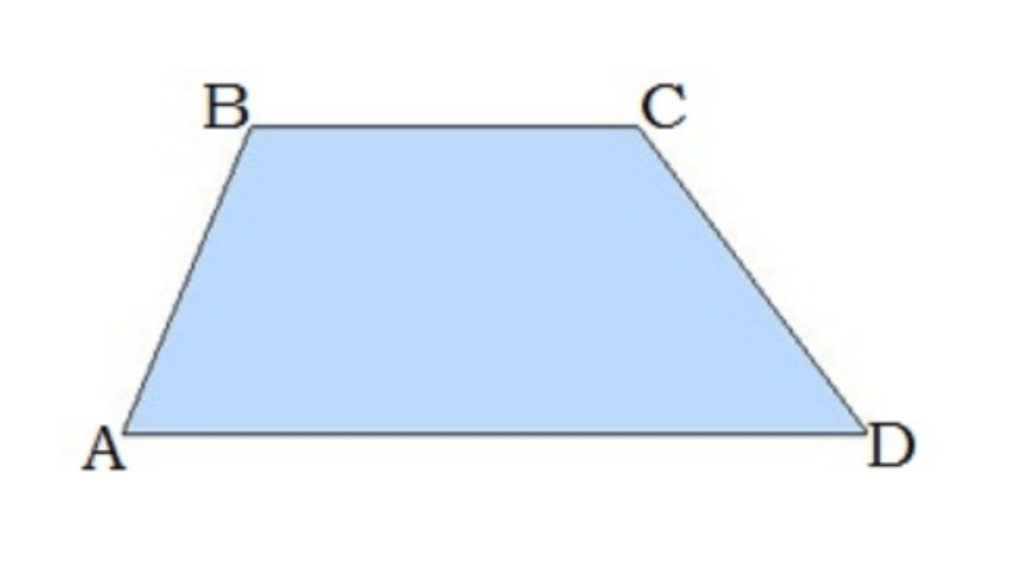
1․ Ո՚ր պատկերն է կոչվում սեղան: GEOGEBRA ծրագրով գծել սեղան:

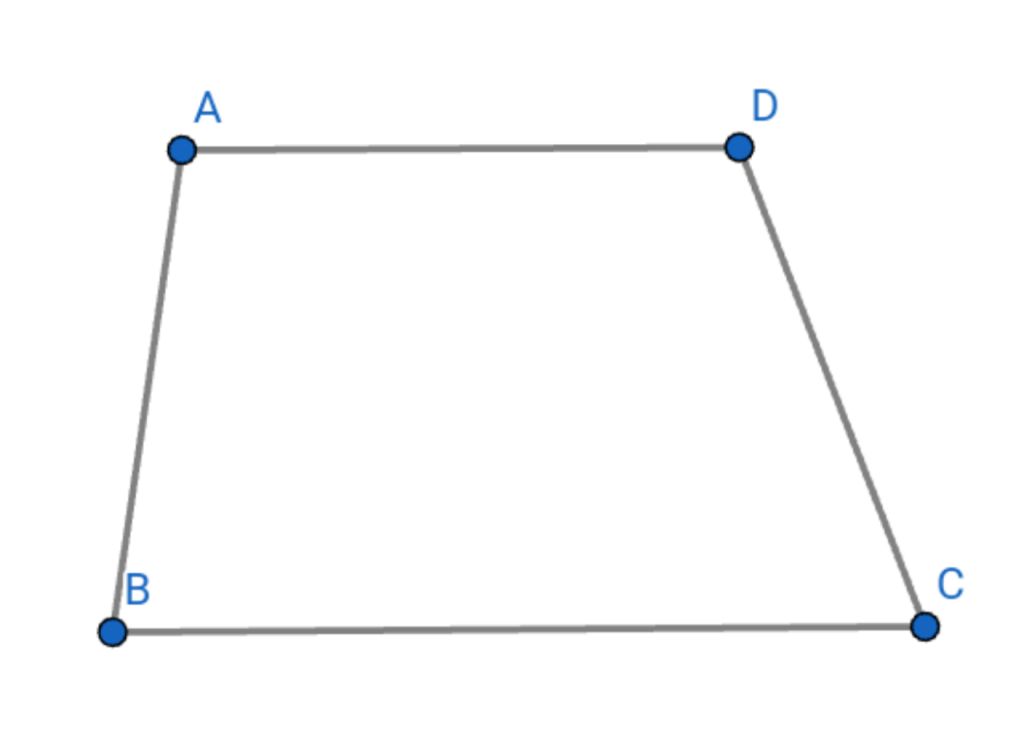
2․Ինչպե՞ս են կոչվում սեղանի կողմերը:

Սեղանի զուգահեռ կողմերը կոչվում են հիմքեր

3․ Ո՚ր պատկերն է կոչվում հավասարասրուն սեղան:

Սեղանը, որի սրունքները հավասար են, կոչվում է հավասարասրուն սեղան:

4․ Թվարկել սեղանի տեսակները: GEOGEBRA ծրագրով գծել այդ պատկերները:

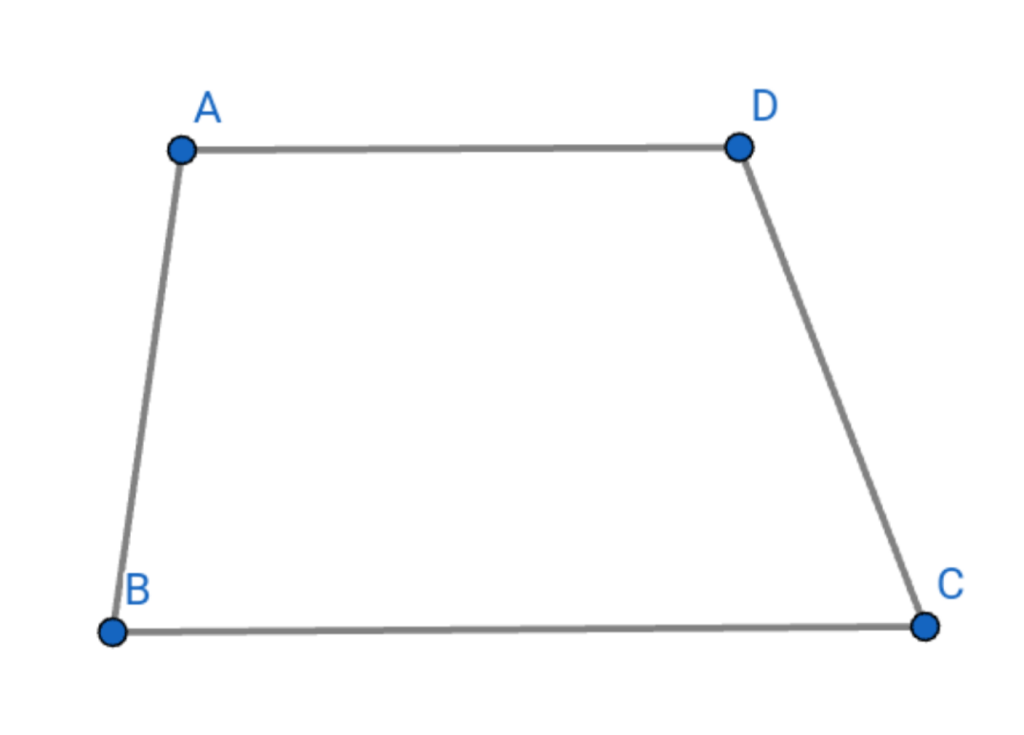
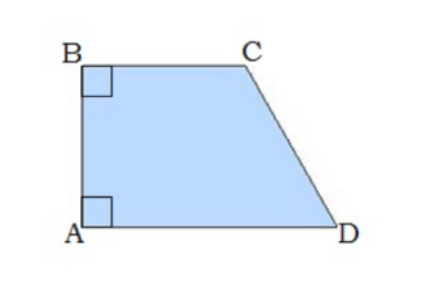
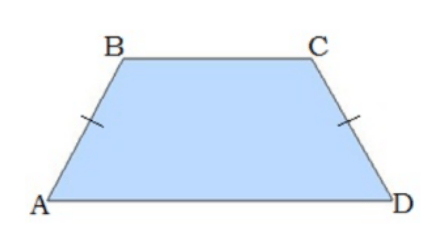
5․ Նշել  ճիշտ պնդումը:

ա) Ցանկացած սեղանի հիմքերը զուգահեռ են:

բ) Հավասարասրուն սեղանի սրունքները զուգահեռ են:

գ) Ուղղանկյուն սեղանի հիմքերը հավասար են:

6․ Տրված է՝ ∢A=37°∢C=121°։ Գտնել ∢B,∢D

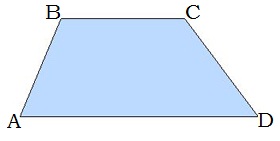
Քանի որ տրված է քառանկյուն, այդ դեպքում քառանկյան ներքին անկյունների գումարը հավասար է 360°-ի.

Այսինքն՝∢A+∢B+∢C+∢D=360°∢A + ∢B + ∢C + ∢D = 360°∢A+∢B+∢C+∢D=360°

Տրված է՝ ∢A = 37° և ∢C = 121°։

Փոխարինենք արժեքները հավասարման մեջ.37°+∢B+121°+∢D=360°37° + ∢B + 121° + ∢D = 360°37°+∢B+121°+∢D=360°

Կատարենք գումարումը.158°+∢B+∢D=360°158° + ∢B + ∢D = 360°158°+∢B+∢D=360°

Այժմ գտնում ենք ∢B + ∢D:∢B+∢D=360°−158°=202°∢B + ∢D = 360° – 158° = 202°∢B+∢D=360°−158°=202°

Այսպիսով, մենք կարող ենք ասել, որ ∢B + ∢D = 202°, սակայն խնդիրը լրացուցիչ տվյալներ չի տրամադրում ∢B և ∢D անկյունները առանձին-առանձին գտնելու համար:

7․ Հաշվել ABCD սեղանի անկյունները, եթե  ∢A=30°

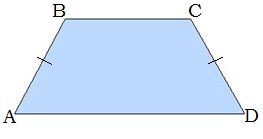
Քառանկյան ներքին անկյունների գումարը միշտ հավասար է 360°-ի.

Եթե ABCD սեղանի անկյուններից մեկը՝ ∢A = 30°, ապա մնացած երեք անկյունների գումարը կլինի հետևյալը.∢A+∢B+∢C+∢D=360°∢A + ∢B + ∢C + ∢D = 360°∢A+∢B+∢C+∢D=360°

Փոխարինելով ∢A = 30°, ստանում ենք.30°+∢B+∢C+∢D=360°30° + ∢B + ∢C + ∢D = 360°30°+∢B+∢C+∢D=360°

Հանում ենք 30°-ը 360°-ից՝∢B+∢C+∢D=360°−30°=330°∢B + ∢C + ∢D = 360° – 30° = 330°∢B+∢C+∢D=360°−30°=330°

Այսպիսով, մնացած երեք անկյունների գումարը պետք է լինի 330°, բայց առանց լրացուցիչ տվյալների, անհնար է գտնել առանձին անկյունների արժեքները (∢B, ∢C, ∢D):

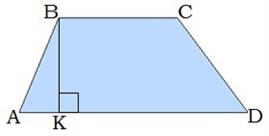
8․ ABCD սեղանի AB սրունքը հիմքի հետ կազմում է 30°: Հաշվիր BK բարձրությունը, եթե AB կողմը 30 սմ է:

9․ Սեղանի հիմքերի հարաբերությունը հավասար է 2:7: Հաշվել սեղանի մեծ հիմքը, եթե նրա փոքր հիմքը հավասար է 12 սմ -ի:

10․ Սեղանի կողմերը հարաբերում են ինչպես՝ 7:6:10:9, իսկ սեղանի պարագիծը 128 սմ է: Հաշվիր սեղանի կողմերը: