
1. 65-5=60
Պատ.թոռնիկ 5տ տատիկ 60տ
2.Եվա
3. 8×2=16
Պատ.16 կաղին
4. 1\4
5. 25+70=95
2)125-95=30
Պատ.30
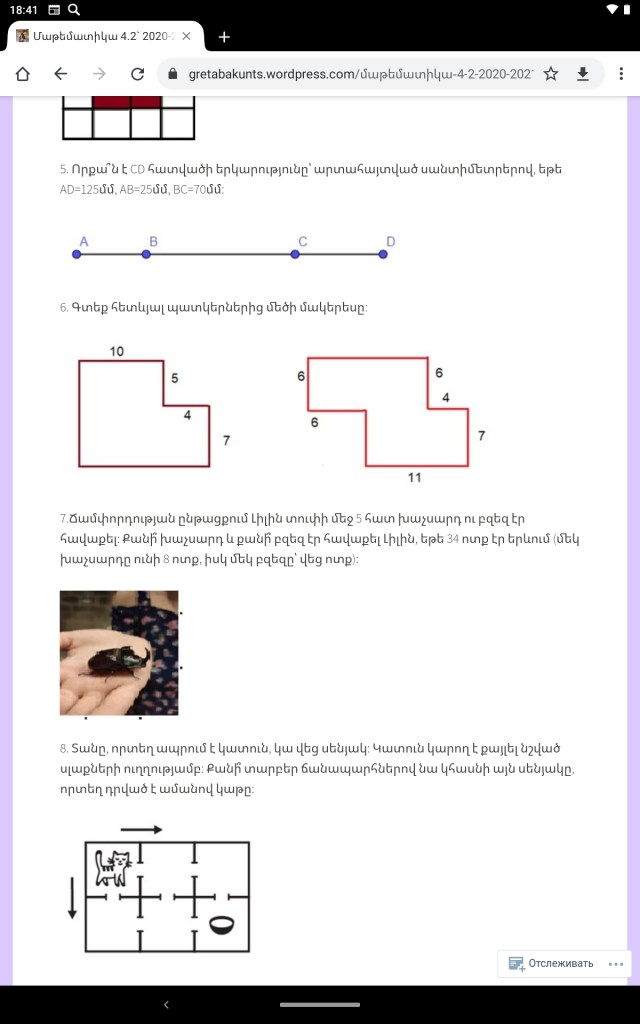
6. 1) 7×11=77
2)6×4=24
3)24+77=101
Պատ.101
7. 2×8=16
3×6=18
16+18=34
Պատ.2 խաչսարդ 3 բզեզ
8. 3 տարբեր ուղղություններով

1. 65-5=60
Պատ.թոռնիկ 5տ տատիկ 60տ
2.Եվա
3. 8×2=16
Պատ.16 կաղին
4. 1\4
5. 25+70=95
2)125-95=30
Պատ.30
6. 1) 7×11=77
2)6×4=24
3)24+77=101
Պատ.101

7. 2×8=16
3×6=18
16+18=34
Պատ.2 խաչսարդ 3 բզեզ
8. 3 տարբեր ուղղություններով
Եթե հայերենի այբուբենը հակառակ հերթականությամբ (ֆ-ից ա) գրենք, ո՞ր տառը կլինի 11-րդը:
Ս տառը
2. Սեպտեմբերի 10-րդ օրը հինգշաբթի է. շաբաթվա ի՞նչ օր կլինի ամսվա 28-րդ օրը:
Երկուշաբթի
3. Գտեք 50-ից մեծ այն երկնիշ թիվը, որը պատիկ է 5-ին, և որի թվանշանների գումարը 8 է:
Սիրելի սովորողներ, 5-ի պատիկ թվերը դրանք այն թվերն են, որնք բաժանվում են 5-ի։
53
4. Քառակուսու պարագիծը 24 սմ է: Գտեք այդ քառակուսու մակերեսը:
Մ-6×4=24սմ
5. Գերանը պետք է սղոցելով բաժանել 10 մասի: Յուրաքանչյուր սղոցումը տևում է 4 րոպե: Քանի՞ րոպեում կավարտվի ամբողջ աշխատանքը:
4×10=40ր
6.«1+2+3+4+5+6+7+8+9» արտահայտության մեջ գումարման նշաններից մեկը փոխարինիր բազմապատկման նշանով այնպես, որ արտահայտության արժեքը ստացվի 100:
7․Մի երկրում կան միայն 7, 8 և 9 թվանշանները: Քանի՞ եռանիշ թիվ կա այդ երկրում:
789-897-987-978-879-798
Բանավոր հաշվարկ՝ բազմապատկման աղյուսակ, ինչպես նաև ոչ մեծ թվերով բանավոր բաժանում։
4.1 և 4․2 դասարանի սիրելի սովորողներ, paint-ով գծեք համապատասխան գծագիրը և լուծեք առաջարկված խնդիրները։ Կարող եք կազմել ու առաջարկել նմանատիպ խնդիրներ։
1․Հաշվի՛ր 15 մմ, 14 մմ, 16 մմ և 17 մմ կողմերով քառանկյան
պարագիծը։
15+14+16+17=62
Պատ.62
2․Հաշվի՛ր 3 դմ, 5 դմ, 8 դմ և 9 դմ կողմերով քառանկյան
պարագիծը։
3+5+8+9=25 դմ
Պատ.25
3․Հաշվիր ուղղանկյան պարագիծը, եթե հայտնի է, որ նրա լայնության և
երկարության գումարը 16 է։
16×2=32
Պատ.32
4․Քառակուսու պարագիծը 28 սմ է։ Որքա՞ն է այդ քառակուսու կողմը։
28÷4=7
Պատ.7
5․Քառակուսու պարագիծը 24 սմ է։ Որքա՞ն է այդ քառակուսու
մակերեսը։
24÷4=6
6×6=36
Պատ.6,36
6․Քառակուսու մակերեսը 81 քառակաուսի մետր է։ Գտի՛ր քառակուսու
կողմը։
9×9=81
Պատ.81
7․Քառակուսու 3 կողմերի գումարը 18 սմ է։ Որքա՞ն է այդ
քառակուսու 1 կողմը։
18÷3=6
Պատ.6
8․Քառակուսու 3 կողմերի գումարը 21 սմ է։ Որքա՞ն է այդ
քառակուսու մակերեսը։
21÷3=7
7×7=49
Պատ.7,49
9․ Ուղղանկյան լայնությունը 5 սմ է, իսկ երկարությունը 4 սմ-ով մեծ է լայնությունից։ Գտնել ուղղանկյան պարագիծը։
5+4=9
Պատ.9
2×5+2×9=10+18=28
10․ Հաշվի՛ր 15սմ և 11 սմ կողմերով ուղղանկյան պարագիծն ու
մակերեսը։
Պ.11+11+15+15=52
Մ.11×15=166
Պատ.52,166
Գտի՛ր քառակուսու մակերեսը և պարագիծը՝ իմանալով, որ նրա կողմի երկարությունը 5 դմ է։
Պ.5×4=20
Մ.5×4=20
Պատ.20
Քառակուսու պարագիծը 28 դմ է։ Գտի՛ր քառակուսու կողմը։
Պ.28÷4=7
Պատ.7
Քառակուսու մակերեսը 49 քառակուսի մետր է։ Գտի՛ր քառակուսու կողմը։
49մ=4900 սմ
4900÷4=1225 սմ
Պատ.1225 սմ
Հաշվի՛ր 25 սմ և 11 սմ կողմերով ուղղանկյան պարագիծն ու մակերեսը:
Պ.25×2=50 11×2=22 50+22=72
25×11=25+25=275
պատ.275
Հաշվիր ուղղանկյան պարագիծը, եթե հայտնի է, որ նրա լայնության և երկարության գումարը 14 սմ է։
Պ.14+14=28
Պատ.28
Հաշվիր ուղղանկյան պարագիծը, եթե հայտնի է, որ նրա լայնության և երկարության գումարը 32 դմ է։
32+32=64
Պատ.64
Ուղղանկյան լայնությունը 8 սմ է, իսկ երկարությունը 2 սմ-ով մեծ է լայնությունից։ Գտնել ուղղանկյան պարագիծը և մակերեսը։
1)2×10=20
2)2×8=16
3)20+16=36
Պ.36
Մ.8×10=80
Պատ. պ.36 մ.80
Հաշվի՛ր 3 դմ, 4 դմ և 5 դմ կողմերով եռանկյան պարագիծը։
Պ.3+4+5=12
Պատ.12
Հաշվի՛ր 15 սմ, 14 սմ, 16 սմ և 17 սմ կողմերով քառանկյան պարագիծը։
15+14+16+17=52
Պատ.52
Սիրելի սովորողներ նախ միասին վերհիշենք, թե ինչպես ենք բազմանիշ թիվը բազմապատկում միանիշ թվով՝
Օրինակ՝
| 1 | ||||
| . | 6 | 4 | 3 | |
| 3 | ||||
| 1 | 9 | 2 | 9 | |
Այժմ փորձենք հասկանալ, թե ինչպես բազմանիշ թիվը բազմապատկենք
երկնիշ թվով։
Թիվը երկնիշ թվով՝ բազմապատկելիս սյունակաձև գրելու դեպքում նախ
այն բազմապատկում ենք միավորով, արդյունքը գրում ենք գծից ներքև 1-ին տողում, ապա տասնավորով, որի արդյունքը գրում ենք երկրոդ տողում 1 նիշ խորքից, և արդյունքները գումարում ենք այնպես, ինչպես այս օրինակներում՝
| . | 4 | 5 | 6 | ||
| 6 | 5 | ||||
| + | 2 | 2 | 8 | 0 | |
| 2 | 7 | 3 | 6 | ||
| 2 | 9 | 6 | 4 | 0 | |
Այժմ փորձենք հասկանալ, թե ինչպես բազմանիշ թիվը բազմապատկենք եռանիշ թվով։
Թիվը եռանիշ թվով բազմապատկելիս սյունակաձև գրելու դեպքում նախ
այն բազմապատկում ենք միավորով, արդյունքը գրում ենք գծից ներքև 1-ին տողում, ապա տասնավորով, որի արդյունքը գրում ենք երկրոդ տողում 1 նիշ խորքից, հետո հարյուրավորով, որի արդյունքը գրում ենք երրորդ տողում 2
նիշ խորքից և արդյունքները գումարում ենք այնպես, ինչպես օրինակում՝
Օրինակ՝
| . | 5 | 4 | 6 | 2 | |||
| 1 | 2 | 3 | |||||
| + | 1 | 6 | 3 | 8 | 6 | ||
| 1 | 0 | 9 | 2 | 4 | |||
| 5 | 4 | 6 | 2 | ||||
| 6 | 7 | 1 | 8 | 2 | 6 | ||
Առաջադրանքներ
4306‧15
| X | 4 | 3 | 0 | 6 | |||||
| 1 | 5 | ||||||||
| + | 2 | 1 | 5 | 3 | 0 | ||||
| 3 | 3 | 0 | 6 | ||||||
| 5 | 4 | 5 | 9 | 0 | |||||
1596·24
| X | 1 | 5 | 9 | 6 | |||||
| 2 | 4 | ||||||||
| + | 6 | 3 | 8 | 4 | |||||
| 3 | 1 | 9 | 2 | ||||||
| 3 | 8 | 2 | 0 | 4 |
1585·153
| X | 1 | 5 | 8 | 5 | |||||
| 1 | 5 | 3 | |||||||
| + | 4 | 7 | 5 | 5 | |||||
| 7 | 9 | 2 | 5 | ||||||
| 1 | 5 | 8 | 5 | ||||||
| 2 | 4 | 2 | 5 | 0 | 5 |
205·104
| X | 2 | 0 | 5 | ||||||
| 1 | 0 | 4 | |||||||
| + | 8 | 2 | 0 | ||||||
| 0 | 0 | 0 | |||||||
| 2 | 0 | 5 | |||||||
| 2 | 1 | 3 | 2 | 0 |
4267‧142
| x | 4 | 2 | 6 | 7 | ||||
| 1 | 4 | 2 | ||||||
| + | 8 | 5 | 3 | 4 | ||||
| 1 | 7 | 0 | 6 | 8 | ||||
| 4 | 2 | 6 | 7 | |||||
| 6 | 0 | 5 | 9 | 1 | 4 |
4628·204
| x | 4 | 6 | 2 | 8 | |||||
| 2 | 0 | 4 | |||||||
| + | 1 | 8 | 5 | 1 | 0 | ||||
| 0 | 0 | 0 | 0 | ||||||
| 9 | 2 | 5 | 6 | ||||||
| 9 | 4 | 4 | 1 | 1 | 0 |
4572·620
| 4 | 5 | 7 | 2 | ||||||
| 6 | 2 | 0 | |||||||
| + | 9 | 1 | 4 | 4 | 0 | ||||
| 1 | 2 | 4 | 3 | 2 | |||||
| 1 | 3 | 3 | 4 | 6 | 4 | 0 |
7058‧25
| X | 7 | 0 | 5 | 8 | |||||
| 2 | 5 | ||||||||
| + | 3 | 5 | 4 | 2 | 5 | ||||
| 1 | 4 | 1 | 1 | 6 | |||||
| 1 | 7 | 6 | 5 | 8 | 5 |
2612‧512
| X | 2 | 6 | 1 | 2 | |||||
| 5 | 1 | 2 | |||||||
| + | 5 | 2 | 2 | 4 | |||||
| 2 | 6 | 1 | 2 | ||||||
| 1 | 3 | 0 | 6 | 0 | |||||
| 1 | 3 | 3 | 7 | 3 | 4 | 4 |
1024‧52
| X | 1 | 0 | 2 | 4 | |||||
| 5 | 2 | ||||||||
| + | 2 | 0 | 4 | 8 | |||||
| 5 | 1 | 2 | 0 | ||||||
| 5 | 3 | 2 | 4 | 8 |
161‧301
| X | 1 | 6 | 1 | ||||||
| 3 | 0 | 1 | |||||||
| + | 1 | 6 | 1 | ||||||
| 0 | 0 | 0 | |||||||
| 4 | 8 | 3 | |||||||
| 4 | 8 | 4 | 6 | 1 |
Սիրելի սովորողներ նախ միասին վերհիշենք, թե ինչպես ենք բազմանիշ թիվը բազմապատկում միանիշ թվով՝
Օրինակ՝
| 1 | ||||
| . | 6 | 4 | 3 | |
| 3 | ||||
| ք1 | 9 | 2 | 9 | |
Այժմ փորձենք հասկանալ, թե ինչպես բազմանիշ թիվը բազմապատկենք
երկնիշ թվով։
Թիվը երկնիշ թվով՝ բազմապատկելիս սյունակաձև գրելու դեպքում նախ
այն բազմապատկում ենք միավորով, արդյունքը գրում ենք գծից ներքև 1-ին տողում, ապա տասնավորով, որի արդյունքը գրում ենք երկրոդ տողում 1 նիշ խորքից, և արդյունքները գումարում ենք այնպես, ինչպես այս օրինակներում՝
| . | 4 | 5 | 6 | ||
| 6 | 5 | ||||
| + | 2 | 2 | 8 | 0 | |
| 2 | 7 | 3 | 6 | ||
| 2 | 9 | 6 | 4 | 0 | |
Այժմ փորձենք հասկանալ, թե ինչպես բազմանիշ թիվը բազմապատկենք եռանիշ թվով։
Թիվը եռանիշ թվով բազմապատկելիս սյունակաձև գրելու դեպքում նախ
այն բազմապատկում ենք միավորով, արդյունքը գրում ենք գծից ներքև 1-ին տողում, ապա տասնավորով, որի արդյունքը գրում ենք երկրոդ տողում 1 նիշ խորքից, հետո հարյուրավորով, որի արդյունքը գրում ենք երրորդ տողում 2
նիշ խորքից և արդյունքները գումարում ենք այնպես, ինչպես օրինակում՝
Օրինակ՝
| . | 5 | 4 | 6 | 2 | |||
| 1 | 2 | 3 | |||||
| + | 1 | 6 | 3 | 8 | 6 | ||
| 1 | 0 | 9 | 2 | 4 | |||
| 5 | 4 | 6 | 2 | ||||
| 6 | 7 | 1 | 8 | 2 | 6 | ||
Առաջադրանքներ
326‧12
| x | 3 | 2 | 6 | ||||||
| 1 | 2 | ||||||||
| + | 6 | 5 | 2 | ||||||
| 3 | 2 | 6 | |||||||
| 3 | 9 | 1 | 2 | ||||||
466·24
| x | 4 | 6 | 6 | ||||||
| 2 | 4 | ||||||||
| + | 1 | 6 | 6 | 4 | |||||
| 9 | 3 | 2 | |||||||
| 1 | 1 | 1 | 8 | 4 | |||||
865·531
| X | 8 | 6 | 5 | ||||||
| 5 | 3 | 1 | |||||||
| + | 8 | 6 | 5 | ||||||
| 2 | 5 | 9 | 5 | ||||||
| 4 | 3 | 2 | 5 | ||||||
| 4 | 5 | 9 | 3 | 1 | 5 |
205·510
| x | 2 | 0 | 5 | ||||||
| 5 | 1 | 0 | |||||||
| + | 2 | 0 | 5 | 0 | |||||
| 1 | 0 | 2 | 5 | ||||||
| 1 | 0 | 4 | 5 | 5 | 0 | ||||
4267‧142
| X | 4 | 2 | 6 | 7 | ||||
| 1 | 4 | 2 | ||||||
| + | 5 | 3 | 4 | |||||
| 1 | 7 | 0 | 6 | 8 | ||||
| 4 | 2 | 6 | 7 | |||||
| 5 | 9 | 7 | 9 | 1 | 4 |
428·204
| x | 4 | 2 | 8 | ||||||
| 2 | 0 | 4 | |||||||
| + | 1 | 7 | 1 | 2 | |||||
| 0 | 0 | 0 | |||||||
| 8 | 5 | 6 | |||||||
| 8 | 7 | 3 | 1 | 2 |
452·420
| X | 4 | 5 | 2 | ||||||
| 4 | 2 | 0 | |||||||
| + | 9 | 0 | 4 | 0 | |||||
| 1 | 8 | 0 | 8 | ||||||
| 1 | 8 | 9 | 8 | 4 | 0 | ||||
2056‧25
| X | 2 | 0 | 5 | 6 | |||||
| 2 | 5 | ||||||||
| + | 1 | 0 | 2 | 8 | 0 | ||||
| 4 | 1 | 1 | 2 | ||||||
| 5 | 1 | 4 | 0 | 0 | |||||
5612‧532
| 5 | 6 | 1 | 2 | ||||||
| 5 | 3 | 2 | |||||||
| + | 1 | 1 | 2 | 2 | 4 | ||||
| 1 | 6 | 8 | 3 | 6 | |||||
| 1 | 7 | 9 | 5 | 8 | 4 | ||||
6024‧62
| x | 6 | 0 | 2 | 4 | |||||
| 6 | 2 | ||||||||
| + | 1 | 2 | 0 | 4 | 8 | ||||
| 3 | 6 | 1 | 4 | 4 | |||||
| 3 | 7 | 3 | 4 | 8 | 8 |
1561‧204
| 1 | 5 | 6 | 1 | ||||||
| 2 | 0 | 4 | |||||||
| + | 6 | 2 | 4 | 4 | |||||
| 0 | 0 | 0 | |||||||
| 3 | 1 | 2 | 2 | ||||||
| 3 | 1 | 8 | 4 | 4 | 4 |
• Եթե տարբերությանը գումարենք հանելին ու ստանանք նվազելին, ապա այն ճիշտ է կատարված, իսկ եթե ոչ, ապա սխալ է։
Նվազելի – հանելի = տարբերություն
4567 – 3569 = 998
1․Կատարենք հանում և այն ստուգենք գումարով.
Օրինակ՝
4567-3569=998
– 4՛ 5՛ 6՛ 7 Ստուգում՝ + 3 5 6 9
3 5 6 9 9 9 8
9 9 8 4 5 6 7
48900-3569=
4 8 9 0 0 Ստ 4 5 3 3 1
– 3 5 6 9 + 3 5 6 9
4 5 3 3 1 4 8 9 0 0
35697-13508=
3 5 6 9 7 Ստ 2 2 1 8 9
– 1 3 5 0 8 + 1 3 5 0 8
2 2 1 8 9 3 5 6 9 7
2000-1598=402
10456-5987=4469
4469+5987=10456
2 0 0 0 Ս տ 1 5 9 8
– 1 5 9 8 + 4 0 2
4 0 2 2 0 0 0
2.Գումարումով ստուգիր ճի՞շտ է արդյոք կատարվել հանումը.
Օրինակ՝ 6999-256=6743 Ստուգում՝
+ 6 7 4 3
2 5 6
6 9 9 9
Ճիշտ է։
25698-5895=19803
1 9 8 0 3
+ 5 8 9 5 Ճ Ի Շ Տ Է
2 5 6 9 8
85694-35698=45996
4 5 9 9 6
+ 3 5 6 9 8
8 1 6 9 4
3.Գտի՛ր անհայտ գումարելին ու կատարիր ստուգում՝
Օրինակ՝
+1569=5694
– 5 6 9՛ 4 Ստուգում՝ + 4 1 2 5
1 5 6 9 1 5 6 9
4 1 2 5 5 6 9 4
+2098=25697
2 5 6 9 7 2 3 5 9 9
– 2 0 9 8 + 2 0 9 8
2 3 5 9 9 2 5 6 9 7
+7856=9086
9 0 8 6 1 2 3 0
– 7 8 5 6 + 7 8 5 6
1 2 3 0 9 0 8 6
8067+ =10789
1 0 7 8 9 2 7 2 2
_ 8 0 6 7 + 8 0 6 7
2 7 2 2 1 0 7 8 9
3805+ =45678
45678-3805=41873 41783+3805=45678
Գումարելի + Գումարելի = Գումար
4156 + 123 = 4279
Գումարման ճշտությունը կարելի է ստուգել հանումով։
• Եթե գումարից հանենք գումարելիներից որևէ մեկը և ստանաք մյուս
գումարելին, ապա գումարման գործողությունը ճիշտ է կատարված,
իսկ եթե ոչ, ապա սխալ է ։
Օրինակ՝ 4156+123=4279
Ստուգում՝ – 4 2 7 9
1 2 3
4 1 5 6
• Հանումով ստուգի՛ր՝ ճիշտ է արդյոք կատարվել գումարումը։
Օրինակ՝ 3695+6984=10679, Ճիշտ է ։
Ստուգում՝
– 1՛ 0՛ 6՛ 7 9
6 9 8 4
3 6 9 5
Առաջադրանքներ
1. Կատարենք գումարում և այն ստուգենք հանումով՝
1549+6995= 8544
8544-1549=6995
3286+7529=10815
10815-3286=7529
6023+8705=14728
14728-8705=6023
123+5962=6085
6085-123=5962
2. Հանումով ստուգի՛ր՝ ճիշտ է արդյոք կատարվել գումարումը։
Օրինակ՝ 3695+6984=10679 : Ճիշտ է ։
Ստուգում՝
– 1՛ 0՛ 6՛ 7 9
6 9 8 4
3 6 9 5
1567+1299=2866 ճիշտ է
2866-1567=1299
1236+9995=13569 սխալ է
13569-1236=12333
1295+369=1664 ճիշտ է
1664-369=1295
1569+984=2569 սխալ է
2569-984=2685
3․ Գտիր անհայտ գումարելին․
Օրինակ՝
+2409 = 6695
– 6 6 9’ 5
2 4 0 9
4 2 8 6
3478+1095 = 4573
4573-1095=3478
2668+618=2686
2686-618=2668
Տրված թվերը ներկայացրենք կարգային միավորների
գումարի տեսքով․
Օրինակ՝
1205=1·1000+2·100+5·1
236=2*100+3*10+6*1
807=8*100+0*10+7*1
4502=4*1000+5*100+0*10+2*1
1561=1*1000+5*100+6*10+1*1
46305=4*10.000+6*1000+3*100+0*10+5*1
75610=7*10.000+5*1000+6*100+1*10+0*1
400693=4*100.000+0*10.000+0*1000+6*100+9*10+3*1
408964=4*100.000+0*10.000+8*1000+9*100+6*10+4*1
Կարգային միավորների գումարը գրիր թվի տեսքով։
Օրինակ՝ 5· 100+3·10+2·1=532
6· 1000+2·100+4·1=6204
8· 1000+6·100+9·10+7·1=8697
4· 1000+3·10+6·1=4036
7· 10000+3·1000+2·10+5·1=70325
4· 10000+3·100+2·10+4·1=40324
3· 10000+3·1000+2·1=33002
6· 100000+3·100+2·10+5·1=600325
3․Ո՞րն է այն վեցանիշ թիվը, որի տասնավորը 8 է, հազարավորը՝ 4, իսկ մյուս բոլոր թվանշանները՝ 9։994980
4․Ո՞րն է այն հնգանիշ թիվը, որի միավորը 2 է, հազարավորը՝ 5, իսկ մյուս բոլոր թվանշանները՝ 1։15112
5․Գտիր այն թիվը, որի միավորը 6 է, տասնավորը 2 անգամ փոքր է միավորից, հազարավորը 0 է, տասհազարավորը՝ 1, հարյուրավորը՝ 3։10336
6․Չորս հազար հինգ հարյուր ութ թիվը թվանշաններով գրելիս, ո՞ր կարգում կլինի «5» թվանշան:3 կարգ
7․Ո՞րն է այն քառանիշ թիվը, որի տասնավորը 4 է, միավորը՝ 5 , մնացած թվանշանները՝ 9։9945
8․Ո՞րն է թվի գրության 2-րդ կարգի կարգային միավորը։Տասնյակ
9․Նշվածներից ո՞րը թվի գրության կարգային միավոր չէ։
10․Քանի՞ երկրորդ կարգի միավոր է պարունակում 4258 թիվը։
11․Ո՞րն է թվի գրության 5-րդ կարգի կարգային միավորը։ Տասհազարյակ
12․Գտիր ամենափոքր քառանիշ և ամենամեծ եռանիշ թվերի տարբերությունը:1000-999=1
13․Գտիր ամենամեծ եռանիշ ու ամենափոքր քառանիշ թվերի գումարից 2-ով մեծ թիվ։999+1000=2001
14․Գտիր ամենափոքր քառանիշ և ամենամեծ հնգանիշ թվերի գումարը։1000+99.999=100.999
15․ 8625 թիվը քանի՞ նիշ ունի և քանի՞ հազարյակ կա հազարյակների կարգում։4 նիշ 8 հազարյակ